Question

Remember that the Pythagorean Theorem gives the sides of a right triangle: a² + b² = c² , wher of the triangle and a and b are the other two sid Use: Pythagorean Theorem to solve the missing II. For # 7-8, find the missing side o #7.

Answer 1

arc functions are the inverse functions of the trigonometric function. So, if we have an angle, for instance, 60°, we can input it to a sin, cos or tan function to get the results:

`\begin{gathered} \sin 60\degree=\frac{\sqrt[]{3}}{2} \\ \cos 60\degree=(1)/(2) \\ \tan 60\degree=\sqrt[]{3} \end{gathered}`

The arc functions, arcsin, arccos and arctan, is the other way around: we have a sin/cos/tan value and want the corresponding angle, so:

`\begin{gathered} \arcsin (\frac{\sqrt[]{3}}{2})=60\degree \\ \arccos ((1)/(2))=60\degree \\ \arctan (\sqrt[]{3})=60\degree \end{gathered}`

9) To find the missing angles, e can use arc functions, the inverse functions of the trigonometric functions.

We have the opposite leg of the angle and the hypotenuse, so we have:

`\begin{gathered} \sin x=(16)/(37) \\ x=\arcsin ((16)/(37))\approx\arcsin (0.4324)\approx25.6\degree \end{gathered}`

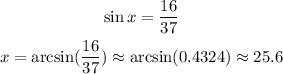
10) We want the adjacent leg, given the angle and the opposite leg, so we use tangent:

`\begin{gathered} \tan 36\degree=(10)/(x) \\ x=(10)/(\tan 36\degree)\approx(10)/(0.7265)=13.8 \end{gathered}`

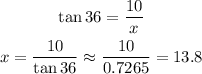
11) Just like 9, we want an angle given its opposite leg and hypotenuse. So we use sine:

`\begin{gathered} \sin x=(8)/(15) \\ x=\arcsin ((8)/(15))\approx\arcsin (0.5333)\approx32.2\degree \end{gathered}`