ANSWER:
(0, 9)
Explanation:
We have the following function:
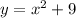
We differentiate with respect to x to calculate the differential of y, like this:
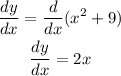
To find out if there is a horizontal line dy/dx is 0, and we solve for x, just like this:
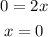
We substitute in the function and get:

Therefore, it has a horizontal tangent line at the point (0, 9)