Question

Two spherical objects have masses of 3.1 x 10^5 kg and 6.5 x 10^3 kg. The gravitational attraction between them is 65 N. How far apart are their centers?

Answer 1

Given data:

* The mass of the first spherical object is,

`m_1=3.1*10^5\text{ kg}`

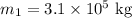
* The mass of the second spherical object is,

`m_2=6.5*10^3\text{ kg}`

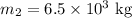
* The force of attraction between the objects is,

`F=65\text{ N}`

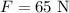
Solution:

The gravitational force of attraction between the spherical object in terms of the distance between their centers is,

`F=(Gm_1m_2)/(d^2)`

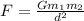
where G is the gravitational constant and d is the distance between the centers of spherical objects,

Substituting the known values,

`\begin{gathered} 65=\frac{6.67*10^(-11)^{}*3.1*10^5*6.5*10^3}{d^2} \\ d^2=(6.67*10^(-11)*3.1*10^5*6.5*10^3)/(65) \\ d^2=2.07*10^(-11+5+3) \\ d^2=2.07*10^(-3) \end{gathered}`

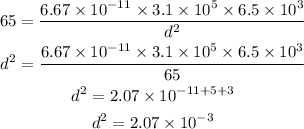
Thus, the distance between the centers is,

`\begin{gathered} d=\sqrt[]{2.07*10^(-3)} \\ d=\sqrt[]{0.207*10^(-2)} \\ d=0.455*10^(-1) \\ d=0.0455\text{ m} \end{gathered}`

Hence, the distance between the centers is 0.0455 meters or 4.6 centimeters.