Question

Find the volume of the con to the nearest 10th period used three. 144 PI. In the last box, type the exponent for the label.

Answer 1

From the question given,

The radius r is

`r=(diameter)/(2)=(8)/(2)=4`

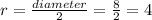
Hence the radius of the cone is 4 in.

The height of the cone is the perpendicular height you see which is 10 in.

Hence the height of the cone is 10 in.

Volume of a cone V is given by the formula

`\begin{gathered} V=(1)/(3)\pi\text{r}^2h \\ where\text{ r = radius = 4 in.} \\ h=\text{ height = 10 in } \\ \pi=3.14 \end{gathered}`

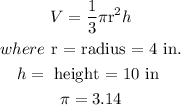
Solving we have

`\begin{gathered} V=(1)/(3)*3.14*4^2*10 \\ V=(1)/(3)*3.14*16*10 \\ V=167.4666 \\ V=167.5\text{ in}^3\text{ to the nearest tenth } \end{gathered}`

Hence Volume of the cone is

`V=167.5\text{ in}^3\text{ }`

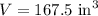
So write it as 167.5 in 3