Question

A bank contains 27 coins in dimes and quarters the coins have a total value of $4.95 find the number of dimes and quarters in the bank show 3 steps identify the veritable set up an equation and solve write a conclusion

Answer 1

First step is to identify the equations.

The phrase, "A bank contains 27 coins in dimes and quartes", tells us that if we add the number of dimes, "d", and the number of quarters, "q", we should have 27 total coins. So the first equation is:

`d+q=27`

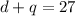
We then have the phrase, "the coins have a total value of $4.95", this implies that if we take the number of dimes and multiply it by the value of one dime and add to the number of quarters multiplied by the value of one quarter we should have a total of $4.95. So we have:

`0.1\cdot d+0.25\cdot q=4.95`

With these two equations we can create a system, as follows:

`\mleft\{\begin{aligned}d+q=27 \\ 0.1\cdot d+0.25\cdot q=4.95\end{aligned}\mright.`

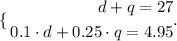
To solve this system we will multiply the first equation by "-0.1" and add the two equations.

`\{\begin{aligned}-0.1\cdot d-0.1\cdot q=-2.7 \\ 0.1\cdot d+0.25\cdot q=4.95\end{aligned}`
`\begin{gathered} -0.1\cdot d+0.1\cdot d-0.1\cdot q+0.25\cdot q=-2.7+4.95 \\ 0.15\cdot q=2.25 \\ q=(2.25)/(0.15)=15 \end{gathered}`

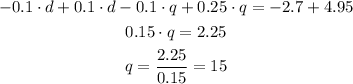
Now that we know the number of quarters we can apply it to the first equation to find the number of dimes, we have:

`\begin{gathered} d+15=27 \\ d=27-15=12 \end{gathered}`

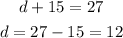
There were 12 dimes and 15 quarters in the bank.