The ratio test says that the series
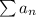
converges if the absolute value of the ratio between consecutive terms approaches a number
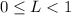
, and diverges otherwise:

You have

Convergence requires that this limit be smaller than 1, so this happens when
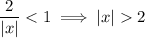
. (This agrees with what you already know about geometric series;
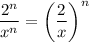
only converges if

.)
The ratio test also works with the second problem.
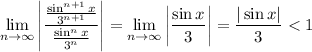

But recall that for all

, you have
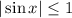
, so the above condition is always met. This means the series converges everywhere.
These first two are also good candidates for using the root test.
For the last two, try the integral test.
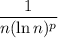
will be positive for all
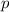
so long as

(

is negative, and so the first term in the series will be negative for any odd
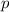
; but we can just omit this term from the series because any one term is still a finite number). So, we compare to the integral,
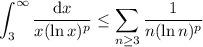
Let
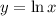
, so that
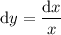
. Then
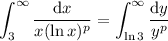
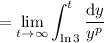
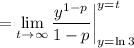

Note that we immediately know
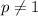
. You have

so the integral converges only for
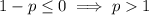
.
For the last one, omit the first two terms (
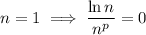
and
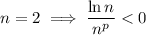
). The remaining sequence is positive and decreasing, which follows from the fact that
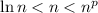
. Then compare to the definite integral,
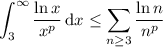
Integrate by parts, setting
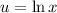
and
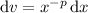
, so that
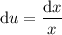
and
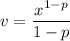
. Then
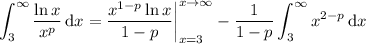
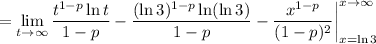
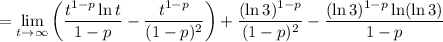
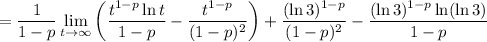
Again, we can't have
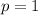
. The integral will converge if the limit converges to a finite number.
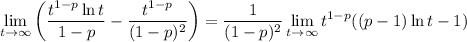
When
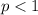
, the limit diverges to
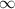
. When

, evaluating the limit directly gives an indeterminate form
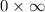
. We rewrite this as
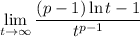
and using the fact that
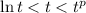
for large enough
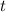
whenever

, it follows that the limit exists by the squeeze theorem. So L'Hopital's rule applies here, and the limit is equal to
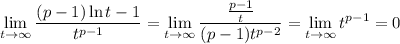
All this to say the last series converges for

.