First, replace f(x) by y. This is done to make the rest of the process easier.
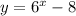
Now, replace every x with y and a every y with an x:

Now, solve this equation for y. Then, we must move -8 to the left hand side as +8. It yields
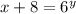
Now, we can apply logarithms in both sides:
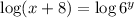
For the properties of logarithms, we have
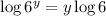
then, we have
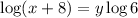
and we obtain
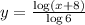
Finally, replace y with f^1. Then, the inverse funcion is
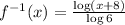
The graphs of the function and its inverse are: