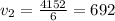Question

two jet leave in Air Base at the same time and travel in opposite directions one jet travel 63 miles an hour faster than the other if the two jets are 7926 miles apart after 6 hours what is the rate of is

Answer 1

we can find the distance of each jet to the Air base and add

distance formula

`d=v* t`

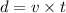
where v is velocity and t the time

First jet

replacing on the formula of the distance, we dont know the velocity so we will assign the letter X, time is 6 hor for the exercise, then

`\begin{gathered} d_1=(x)*(6) \\ d_1=6x_{} \end{gathered}`

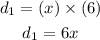
First distance is represented by 6x

Second jet

We apply the formula, where velocity is 63 miles an hour faster than the other, and the same time 6 hours

`\begin{gathered} d_2=(x+63)*(6) \\ d_2=6x+378 \end{gathered}`

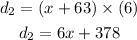
Solving x

now we sum the distances and the solution is total distance(7926miles)

`\begin{gathered} d_1+d_2=7926 \\ 6x+6x+378=7926 \\ 12x+378=7926 \end{gathered}`

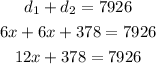
and we can find the missing number (x, velocity of first jet)

`\begin{gathered} 12x=7926-378 \\ 12x=7548 \\ x=(7548)/(12) \\ \\ x=629 \end{gathered}`

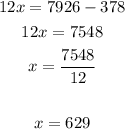
Finally

we can calculate the rate or velocity of each jet

first jet

`\begin{gathered} d_1=6x \\ d_1=6(629) \\ d_1=3774 \end{gathered}`

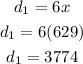
and find the rate or velocity dividing disntace between time

`v_1=(3774)/(6)=629`

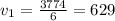
Second jet

`\begin{gathered} d_2=6x+378 \\ d_2=6(629)+378 \\ d_2=3774+378 \\ d_2=4152 \end{gathered}`

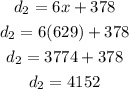
and find the rate or velocity

`v_2=(4152)/(6)=692`