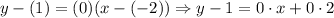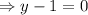Question

The graph of a line passes through the two points (-2, 1) and (2, 1). What is the equation of the line written in general form?answers:•x+y1=0•y-1=0•x-y+1 = 0

Answer 1

We will have the following:

First, we find the slope:

`m=(1-1)/(2-(-2))\Rightarrow m=0`

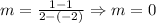
So, the equation that represents the line is:

`y=1`

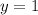
So:

`y-1=0`

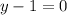
***Explanation***

We are given the points (-2, 1) & (2. 1).

From this we cans see that the line passes both times through y = 1.

We also know that the slope (m) is given by:

`m=(y_2-y_1)/(x_2-x_1)`

So the slope for this line will be:

`m=(1-1)/(2-(-2))\Rightarrow m=0`

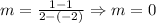
Now, we also know that the equation of the line in general form is given by:

`y-y_1=m(x-x_1)`

So, the equation of the line will be given by:

`y-1=(0)(x+2)\Rightarrow y-1=0`

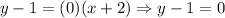
So the function is a constant value, thus a horizontal line.

***Explanation for the general form of a line***

The general form of a line is given by:

`y-y_1=m(x-x_1)`

Here "x" & "y" are two variables; "x1" & "y1" are the component of a point that belongs to that lline and "m" is the slope of that line. We remember that (x1, y1) can be any point that belongs to the line.

So, we simply replace the values, in our case I willl solve for (-2, 1), but we could also use (2, 1), the solution at the end will be the same.

So:

`y-(1)=(0)(x-(-2))\Rightarrow y-1=0\cdot x+0\cdot2`
`\Rightarrow y-1=0`