Question

Define f(x =x2 if x <0 and f(x =x x2 if x>=0. differentiation gives f''(x2. this is bogus. why

Answer 1

`f(x)=\begin{cases}x^2&\text{for }x<0\\x+x^2&\text{for }x\ge0\end{cases}`


`f'(x)=\begin{cases}2x&\text{for }x<0\\f'(0)&\text{for }x=0\\1+2x&\text{for }x>0\end{cases}`

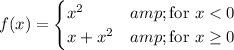
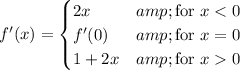
In order for
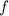
`f` to be differentiable at
`x=0`, i.e. for
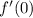
`f'(0)` to exist, the limit from either side of
`x=0` of
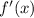
`f'(x)` must be the same. This is not the case, as


`\displaystyle\lim_(x\to0^-)f'(x)=\lim_(x\to0^-)2x=0`

`\displaystyle\lim_(x\to0^+)f'(x)=\lim_(x\to0^+)(1+2x)=1`

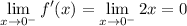
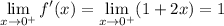
and so
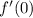
`f'(0)` does not exist.

Meanwhile,


`f''(x)=\begin{cases}2&\text{for }x<0\\f''(0)&\text{for }x=0\\2&\text{for }x>0\end{cases}`

where


`f''(0)=\displaystyle\lim_(x\to0)(f'(x)-f'(0))/(x-0)=\lim_(x\to0)\frac{f'(x)-f'(0)}x`

But we found that
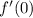
`f'(0)` doesn't exist, so this limit also can't exist, which in turn means that
`f''(0)` does not exist.

On the other hand,
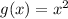
`g(x)=x^2` is continuous and differentiable everywhere, so that
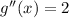
`g''(x)=2`, and in particular,
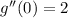
`g''(0)=2`.