Question

How to evaluate infinite series 1/n

Answer 1

This series diverges.


`\displaystyle\sum_(n\ge1)\frac1n`

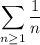
Notice that this series essentially gives the left-endpoint Riemann sum approximation to the integral


`\displaystyle\int_1^\infty\frac{\mathrm dx}x`

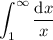
Because
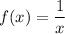
`f(x)=\frac1x` is strictly decreasing for
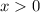
`x>0`, it follows that this approximation is greater than or equal to the value of the integral:


`\displaystyle\sum_(n\ge1)\frac1n\ge\int_1^\infty\frac{\mathrm dx}x`

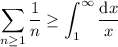
So if the integral diverges, then so must the finite series. You have


`\displaystyle\int_1^\infty\frac{\mathrm dx}x=\lim_(t\to\infty)\int_1^t\frac{\mathrm dx}x=\ln|x|\bigg|_(x=1)^(x=t)`

`=\displaystyle\lim_(t\to\infty)\ln|t|=\infty`

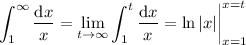
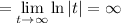
and thus the series must also diverge.