Question

An object is suspended from two cables that meet at a point above the object. One cable pulls with a force modeled by F1 = −77i + 35j. The other cable pulls with a force modeled by F2 = 92i + 84j. What is the angle between the cables? Round to the nearest degree.

Answer 1

`113\degree`

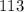
Step-by-step explanation

To find the angle between the two forces, we have to apply the formula for the dot product of two vectors:

`\begin{gathered} F_1\cdot F_2=|F_1|\cdot|F_2|\cdot\cos \theta \\ \Rightarrow\cos \theta=(F_1\cdot F_2)/(|F_1|\cdot|F_2|) \end{gathered}`

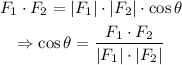
where θ = angle between the forces

Let us find the dot product of the two forces:

`\begin{gathered} F_1\cdot F_2=(-77i+35j)\cdot(92i+84j) \\ F_1\cdot F_2=(-77\cdot92)+(35\cdot84) \\ F_1\cdot F_2=-7084+2940 \\ F_1\cdot F_2=-4144 \end{gathered}`

Now, let us find the magnitude of the two vectors.

For F1:

`\begin{gathered} \lvert F_1\rvert=\sqrt[]{(-77)^2+(35)^2} \\ \lvert F_1\rvert=\sqrt[]{5929+1225}=\sqrt[]{7154} \\ \lvert F_1\rvert=84.58 \end{gathered}`

For F2:

`\begin{gathered} \lvert F_2\rvert=\sqrt[]{(92)^2+(84)^2} \\ \lvert F_2\rvert=\sqrt[]{8464+7056}=\sqrt[]{15520} \\ \lvert F_2\rvert=124.58 \end{gathered}`

Now, substitute all the calculated values into the dot product equation obtained above:

`\begin{gathered} \cos \theta=(-4144)/(84.58\cdot124.58) \\ \cos \theta=(-4144)/(10536.98)=-0.3933 \end{gathered}`

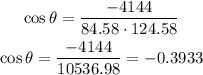
Solve for θ:

`\begin{gathered} \theta=\cos ^(-1)(-0.3933) \\ \theta=113\degree \end{gathered}`

That is the angle between the forces.