Question

I really need help solving this practice from my ACT prep guide

Answer 1

The question is given below as

`\tan \mleft((\pi)/(3)\mright)+\sin \mleft((5\pi)/(6)\mright)\cos \mleft(-(3\pi)/(4)\mright)`

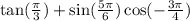
Step 1:

Using the following identity below

`\sin \mleft(x\mright)=\cos \mleft((\pi)/(2)-x\mright)`

By applying the identity above, we will have

`\begin{gathered} \sin \mleft((5\pi)/(6)\mright)=\cos \mleft((\pi)/(2)-(5\pi)/(6)\mright) \\ \sin ((5\pi)/(6))=\cos ((3\pi-5\pi)/(6)) \\ \sin ((5\pi)/(6))=\cos (-(2\pi)/(6)) \\ \sin ((5\pi)/(6))=\cos (-(\pi)/(3)) \end{gathered}`

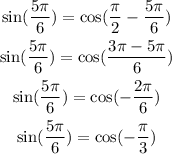
Step 2:

Use the property below

`\cos \mleft(-x\mright)=\cos \mleft(x\mright)`

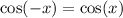
By applying the property above, we will have

`\begin{gathered} \cos \mleft(-(\pi)/(3)\mright)=\cos \mleft((\pi)/(3)\mright) \\ \cos \mleft(-(3\pi)/(4)\mright)=\cos \mleft((3\pi)/(4)\mright) \end{gathered}`

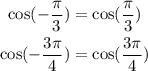
The question above then becomes

`\begin{gathered} \tan ((\pi)/(3))+\sin ((5\pi)/(6))\cos (-(3\pi)/(4)) \\ \tan ((\pi)/(3))+\cos ((\pi)/(3))\text{.}\cos ((3\pi)/(4)) \end{gathered}`

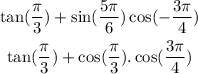
Using the following trivial identities, we will have

`\begin{gathered} \tan \mleft((\pi)/(3)\mright)=√(3) \\ \cos \mleft((\pi)/(3)\mright)=(1)/(2) \\ \cos ((3\pi)/(4))=\frac{-\sqrt[]{2}}{2} \end{gathered}`

By substituting the above trivial identities, we will have

`\begin{gathered} \tan ((\pi)/(3))+\cos ((\pi)/(3))\text{.}\cos ((3\pi)/(4)) \\ \sqrt[]{3}+(1)/(2)*\frac{-\sqrt[]{2}}{2} \\ =\sqrt[]{3}-\frac{\sqrt[]{2}}{4} \\ =\frac{4\sqrt[]{3}-\sqrt[]{2}}{4} \end{gathered}`

Hence,

The SECOND OPTION is the right answer

`\frac{4\sqrt[]{3}-\sqrt[]{2}}{4}`