When
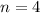
, you have
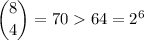
but when
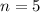
, you have
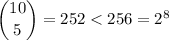
so
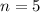
is the base case.
Assume the relation holds for
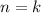
, i.e.
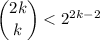
To show that it holds for
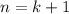
, notice that
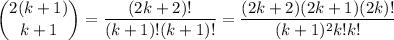
Since
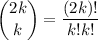
, it must be the case that
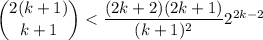
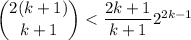
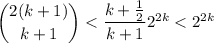
where the last line follows from the fact that the numerator is necessarily smaller than the denominator in
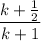
.