The calculation shows that the measure of the angle represented by x is approximately
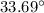 , which is closest to 34°.
, which is closest to 34°.
Sure, to find the angle x, we use the tangent function based on the sides of the right-angled triangle formed by Sid's directions.
Given:
Opposite side (height) = 2 miles
Adjacent side (base) = 3 miles
The formula for the tangent of an angle in a right triangle is:
![\[\tan(x) = \frac{\text{Opposite}}{\text{Adjacent}} = (2)/(3)\]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/hzcuaptbg5t2v0cxocvi.png)
To find x, take the arctangent (inverse tangent) of both sides:
![\[ x = \tan^(-1)\left((2)/(3)\right) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/fjs5ulfavjjnky0c6wc4.png)
Using a calculator:
![\[ x \approx \tan^(-1)\left((2)/(3)\right) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/9slu62oieskclctstcj1.png)
![\[ x \approx 33.69^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/o8rarmz3knzftzm4heyd.png)
![\[33.69^\circ \approx 34^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/dexk6hgtfwoc9jrpmxb0.png)