Answer
(a) 63.3%
(b) 72.7%
(c) 28.7%
Step-by-step explanation
Given:
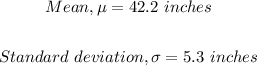
(a) What percentage of years will have an annual rainfall of less than 44 inches?
First, we standardize 44 inches by changing x to z:
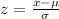
Here,
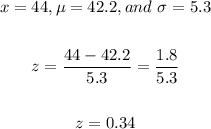
So,
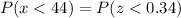
Interpreting the result in a normal curve, we have:
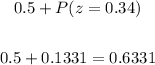
Therefore, the percentage to the nearest tenth will be:
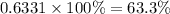
(b) What percentage of years will have an annual rainfall of more than 39 inches?
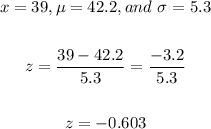
So,
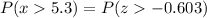
Interpreting the result in a normal curve, we have:
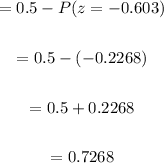
Therefore, the percentage to the nearest tenth will be:
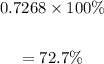
(c) What percentage of years will have an annual rainfall of between 38 inches and 43 inches?
We need to find P(39 ≤ x ≤ 43).
Standardizing x to z by applying:
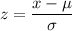
Here,
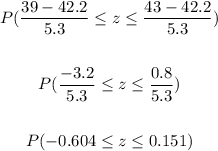
Also, interpreting the result in a normal curve, we have:
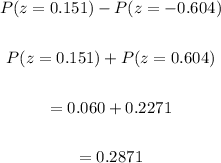
Hence, the percentage to the nearest tenth will be:

In summary,
(a) 63.3%
(b) 72.7%
(c) 28.7%