First, let's start from the left with the angle that measures 88º and ∠1 (green line)
These two angles are a linear pair, which means that they add up to 180º, you can express it as:

From this expression, you can calculate the measure of ∠1, just subtract 88º from 180º
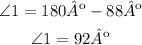
∠1=92º
Second, the ∠5 and the angle that measures 81º. These angles are between two parallel lines crossed by a transversal line. The lines that link them make a Z shape (purple line).
These angles are alternate interior angles which makes them congruent, we can conclude that
∠5=81º
Third, from the triangle on the right we know 2 of its three angles and we know that the sum of the inner angles equals 180º, so we can calculate the missing angle as follows:
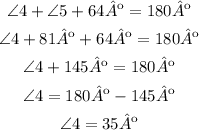
∠4=35º
Fourth, ∠3, ∠4 and, the angle that measures 81º are supplementary angles (red line), which means that they add up to 180º, therefore you can calculate ∠3 as follows:
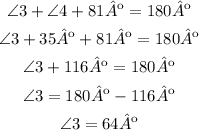
∠3=64º
Fifth, ∠1, ∠2 and, ∠3 are the inner angles of the triangle on the left so they add up to 180º.
You can calculate ∠2 as follows:
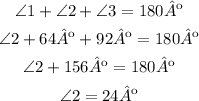
∠2=24º
So
∠1=92º
∠2=24º
∠3=64º
∠4=35º
∠5=81º