Question

A particle that started at the origin and is moving along thex-axis has a velocity function given by

Answer 1

The function given in the question is

`v(t)=\frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}}`

Concept: To calculate the particle position of the function above, we will have to find the anti-derivative of the function above

`x(t)=\int v(t)`

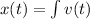
By substituting the values, we will have

`\begin{gathered} x(t)=\int v(t) \\ x(t)=\int \frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}} \end{gathered}`

Step 1: Spilt the function using the law of integration of addition

`\int \frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}}=\int \frac{1}{\sqrt[]{t+9}}+\int \frac{\sqrt[]{t+9}}{\sqrt[]{t+9}}`

Step 2: The equation above becomes

`\int \frac{1}{\sqrt[]{t+9}}+\int \frac{\sqrt[]{t+9}}{\sqrt[]{t+9}}=\int \frac{1}{\sqrt[]{t+9}}+\int 1`

Step 3: Integrate the expression below using integration by substitution

`\begin{gathered} \int \frac{1}{\sqrt[]{t+9}}dt \\ \text{let } \\ u=t+9 \\ (du)/(dt)=1 \\ du=dt \end{gathered}`
`\begin{gathered} \int \frac{1}{\sqrt[]{u}}du=\int u^{-(1)/(2)}du=\frac{u^{-(1)/(2)+1}}{-(1)/(2)+1}=u^{(1)/(2)}/(1)/(2)=2u^{(1)/(2)}=2\sqrt[]{u}=2\sqrt[]{t+9} \\ \int 1=t \end{gathered}`
`\int \frac{1}{\sqrt[]{t+9}}+\int 1=2\sqrt[]{t+9}+t+c`
`x(t)=2\sqrt[]{t+9}+t+c`

To calculate the value of constant c., since it is starting from the origin, we will have

`(0,0)=(t,x)`
`x(0)=0`
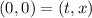
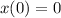
`\begin{gathered} x(t)=2\sqrt[]{t+9}+t+c \\ 0=2\sqrt[]{0+9}+0+c \\ 0=2\sqrt[]{9}+c \\ 0=6+c \\ c=0-6 \\ c=-6 \end{gathered}`

Replace the value of c in the function of x(t)

`\begin{gathered} x(t)=2\sqrt[]{t+9}+t+c \\ x(t)=2\sqrt[]{t+9}+t-6 \end{gathered}`

At t=16, we will have the particle position be

`\begin{gathered} x(t)=2\sqrt[]{t+9}+t-6 \\ x(16)=2\sqrt[]{16+9}+16-6 \\ x(16)=2\sqrt[]{25}+10 \\ x(16)=2*5+10 \\ x(16)=10+10 \\ x(16)=20 \end{gathered}`