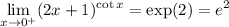where
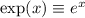
.
By continuity of

, you have
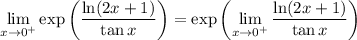
As
in the numerator, you approach
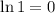
; in the denominator, you approach
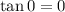
. So you have an indeterminate form

. Provided the limit indeed exists, L'Hopital's rule can be used.
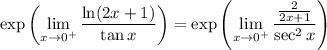
Now the numerator approaches

, while the denominator approaches
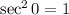
, suggesting the limit above is 2. This means