Question

Graph triangle RST with verticles R(4,1) S(7,3) T(6,4) and its image after the 2 transformations. 1) Translation: (x,y) (x-3,y) 2)Reflections: reflect across y=-1

Answer 1

First we draw the original triangle with vertexes R(4,1), S(7,3) and T(6,4).

Now we need to find the vertexes for the new triangle. We know that first we do the translation

`(x,y)\rightarrow(x-3,y)`

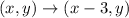
then the points will translate as follows:

`\begin{gathered} (4,1)\rightarrow(1,1) \\ (7,3)\rightarrow(4,3) \\ (6,4)\rightarrow(3,4) \end{gathered}`

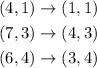
Now we need to perform the reflection across the line y=-1. To do this we have to remember that a reflection across a line of the form y=k is defined by

`(x,y)\rightarrow(x,2k-y)`

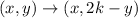
In our case we have k=-1, then:

`\begin{gathered} (1,1)\rightarrow(1,-2-1)=(1,-3) \\ (4,3)\rightarrow(4,-2-3)=(4,-5) \\ (3,4)\rightarrow(3,-2-4)=(3,-6) \end{gathered}`

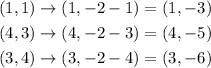
Then the vertexes of the new triangle are R'(1,-3), S(4,-5) and (3,-6). Drawing them in the plane we have.