Answer:
The correct option is A.
Explanation:
The standard from of a circle is
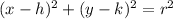
Where, (h,k) is center of the circle and r is the radius.
It is given that the center of the circle is (3,8) and the radius of the circle is 5 units.
Substitute h=3, k=8 and r=5 in the above equation .
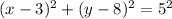

![[\because (x-y)^2=x^2-2xy+y^2]](https://img.qammunity.org/2018/formulas/mathematics/high-school/mo0tdiwc4u68r1wernkne9ff6b6oszc15z.png)


Subtract 25 from both the sides.
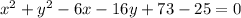
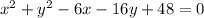
Therefore the correct option is A.