Answer:
A rational expression is an expression of the form a/b. If we want at least one x in the denominator, we can write the following
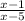
Part a.
If we make the expression equal to 0 and we solve, we get:
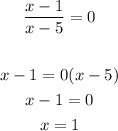
So, it has a solution because the numerator is equal to 0 when x = 1 and x = 1 doesn't make the denominator equal to 0.
Part b.
If we make the expression equal to y, we get:
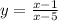
Then, the graph of the expression is
So, the expression doesn't have a value for x = 5 and it doesn't have a value of x that makes y = 1.
Part c.
The expression doesn't have a value for x = 5 because the denominator is equal to 0 at x = 5 and it doesn't have a value of x that makes y = 1 because there is no solution to the equation
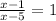
Part d.
If we add 6 to the denominator, we get the following expression
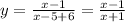
Then, the graph is
Therefore, we can see that the vertical asysmptote change from x = 5 to x = -1 because the denominator change from x = -5 to x = 1.