Question

Answer if you know

this is calculus so don't put idk or whatever
show all work and resons


the reigon R is bounded by the x axis,the y axis and y=√x and y=6-x
the area of the reigon is 22/3
the reigon R is the base of a solid. for every y, where 0≤y≤2, the cross section of the solid taken perpendicular to the y axis is a rectangle whose base lies in R and whose heigh is is 2y. write, but do not evaluate, and integral expression that gives the volume of the solid

Answer 1

I've attached a plot of one such cross-section (orange) over the region in the x-y plane (blue), including the bounding curves (red). (I've set
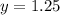
`y=1.25` for this example.)

The length of each cross section (the side lying in the base) has length determined by the horizontal distance
`x` between the y-axis
`x=0` and the curve
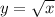
`y=\sqrt x`. In terms of
`y`, this distance is
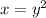
`x=y^2`. The height of each cross section is twice the value of
`y`, so the area of each rectangular cross section should be
`2y^3`.

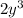
This means the volume would be given by the integral


`\displaystyle\int_0^22y^3\,\mathrm dy`