Question

`(dy)/(dx)= (8cos(x))/( x^(2) ) - (1)/(8)`

How many relative maxima and how many relative minima are there on the interval (1,10)? I don't see the way forward so I did some handwaving and said that the function in terms of maxima and minima is driven by cos(x). Since cos(x) has 2 minima and one maximum on that interval, I claimed that the function also must have 2 minima and 1 max.

Is there an analytical way to answer this?

Answer 1

Intermediate value theorem.

Extrema occur at points where
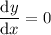
`(\mathrm dy)/(\mathrm dx)=0`, with maxima occurring at
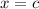
`x=c` if the derivative is positive to the left of
`c` and negative to the right of
`c`, and minima in the opposite case.

So suppose you take two values
`a,b`. If it turns out that
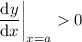
`(\mathrm dy)/(\mathrm dx)\bigg|_(x=a)>0` and
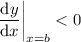
`(\mathrm dy)/(\mathrm dx)\bigg|_(x=b)<0`, then the IVT guarantees the existence of some
`c\in(a,b)` such that
`(\mathrm dy)/(\mathrm dx)\bigg|_(x=c)=0`.

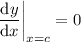
Choosing arbitrary values of
`a,b` won't guarantee that exactly one such
`c` exists, though. The function could easily oscillate several more times between
`a` and
`b`, intersecting the x-axis more than once, for example. This is where your suspicion can be applied. Knowing that
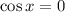
`\cos x=0` for
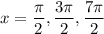
`x=\frac\pi2,\frac{3\pi}2,\frac{7\pi}2` (approximately 1.57, 4.71, 7.85, respectively), you can use these values as reference points for computing the sign of the derivative.

When
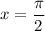
`x=\frac\pi2`, you have
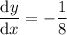
`(\mathrm dy)/(\mathrm dx)=-\frac18`. You know that
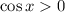
`\cos x>0` for
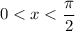
`0<x<\frac\pi2`, and that as
`x\to0^+`,
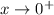
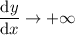
`(\mathrm dy)/(\mathrm dx)\to+\infty`. This means there must be some
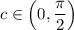
`c\in\left(0,\frac\pi2\right)` such that
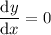
`(\mathrm dy)/(\mathrm dx)=0`, and in particular, this value of
`c` is the site of a relative maximum.

You can use similar arguments to determine what happens at the other two suspected critical points.