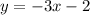Question

5) Write the equation of the line below using the rise over run method. Write theequation in slope-intercept form.

Answer 1

First we need to find the slope of the line. Using the rise over run method, we can see that the change in the y axis (rise) is negative, and if we see the difference in y axis is 3 units between the points (-2, 4) and (-1, 1). The run is the change in the horizontal axis. We can see that the difference is 1.

Then:

Rise = -3

Run = 1

`\text{slope}=(-3)/(3)=-3`

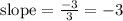
The slope is -3.

The equation of a line given a point and the slope is:

`y-y_0=m(x-x_0)`

Where m is the slope and x1, y0 are the coordinates of a point.

If we take the point (-1, 1), and the slope = -3:

`y-1=-3(x-(-1))`

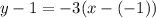
Now if we solve for y, we get the equation of the line in slope-intercept form:

`\begin{gathered} y=-3(x+1)+1 \\ y=-3x-3+1 \\ y=-3x-2 \end{gathered}`

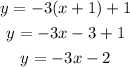
The equation of the line in spoe intercept form is:

`y=-3x-2`