Question

Prove that the value of the expression a^2–a is divisible by 2 for any whole value of a.

Answer 1

Answer with explanation:

To prove:
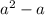`a^2-a` is divisible by 2 for any whole value of a.

Consider
`a^2-a=a(a-1) \ \ \ \ [\text{ Taking 'a' out as common }]`

Here, a and (a-1) are two consecutive numbers such that,

either of them must be an odd number and an even number.

i.e. a(a-1)= Product of even and an odd number = Even number [Trivial statement]

⇒ a(a-1) is divisible by 2 [Every even number is divisible by 2.]

⇒
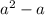`a^2-a` is divisible by 2 for any whole value of a.

Hence proved.