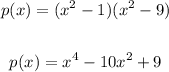Question

A) List the roots and it’s multiplicity.B) domain and range C) equation (show work by solving for a)

Answer 1

First, let's list the roots, we can see in the graph that it's

`\begin{gathered} z_1=-1 \\ z_2=1 \\ z_3=-3 \\ z_4=3 \end{gathered}`

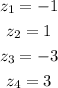
We can see that the graph crosses the x-axis on all roots then they all have simple multiplicity (1). Then we know that the polynomial is something like

`\begin{gathered} p(x)=a(x-z_1)(x-z_2)(x-z_3)(x-z_4) \\ \\ p(x)=a(x+1)(x-1)(x+3)(x-3) \end{gathered}`

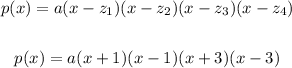
We can find the domain and the range graphically, we know that polynomial functions do not have any domain restriction, therefore

`\text{ domain = }\mathbb{R}`

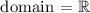
For the range, we must see which values the polynomial can take, usually, even powered polynomials have a restricted range, here the degree is 4, then it must be restricted.

We can see in the graph that the function does not take any value under -16, therefore the range is

`\text{ range = \textbraceleft y }\ge\text{ -16\textbraceright}`

___________________________________

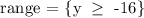
Now to find the equation, let's remember that

`p(x)=a(x+1)(x-1)(x+3)(x-3)`

We do not have the value of "a", but we know that when x = 0 we have y = 9, we can use that to find a

`\begin{gathered} 9=a(0+1)(0-1)(0+3)(0-3) \\ \\ 9=a\cdot9 \\ \\ a=(9)/(9) \\ \\ a=1 \end{gathered}`

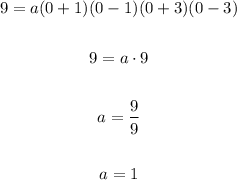
Therefore the equation is

`p(x)=(x+1)(x-1)(x+3)(x-3)`

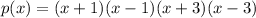
We can also do the distributive

`\begin{gathered} p(x)=(x^2-1)(x^2-9) \\ \\ p(x)=x^4-10x^2+9 \end{gathered}`