Question

Triangles ACD and BCD are isosceles. Angle BAC has a measure of 17degrees and angle BDC has a measure of 52 degrees. The measure ofangle ABD is degrees.

Answer 1

Step-by-step explanation

We want to find the measure of We are given that:

`\begin{gathered} <\text{BAC}=17\degree \\ <\text{BDC}=52\degree \end{gathered}`

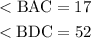
Triangle BDC is an isosceles triangle. This means that:

`<\text{BDC}=<\text{BCD}`

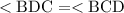
We need to find the measure of apply the sum of angles in a triangle:

`\begin{gathered} <\text{BDC}+<\text{BCD}+<\text{CBD}=180 \\ \Rightarrow52+52+<\text{CBD}=180 \\ 104+<\text{CBD}=180 \\ \Rightarrow<\text{CBD}=180-104 \\ <\text{CBD}=76\degree \end{gathered}`

From the figure, we see that triangle ABC and ABD are congruent triangles. This means that all three sets of angles in the triangles are congruent (equal in measure).

Therefore:

`<\text{ABC}=<\text{ABD}`

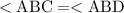
The sum of angles at a point is equal to 360 degrees. This means that:

`<\text{ABC}+<\text{ABD}+<\text{CBD}=180`

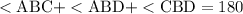
Since angles