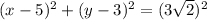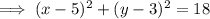Question

If the endpoints of the diameter of a circle are (8, 6) and (2, 0), what is the standard form equation of the circle?

Answer 1

18 = (x-5)^2 + (y-3)^2

Answer 2

Answer:
`(x-5)^2+(y-3)^2=18`

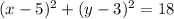
Explanation:

Here, the endpoints of the diameter of a circle are (8, 6) and (2, 0),

The center of the circle = Mid point of the line segment that shows the diameter

= Mid point of (8, 6) and (2, 0),

=
`((8+2)/(2), (6+0)/(2))`

=
`((10)/(2),(6)/(2))`

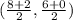
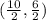
= ( 5, 3 )

Now, the diameter of the circle = Distance of the points (8,6) and (2,0)

=
`√((2-8)^2+(0-6)^2)`

=
`√(6^2+6^2)`

=
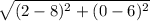
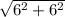
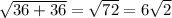`√(36+36)=√(72)=6√(2)` unit

⇒ The radius of the circle = 3√2 unit

Since, the standard form equation of the circle is (x-h)² + (y-k)² = r²

Where (h,k) is the center of the circle and r is the radius of the circle,

Hence, The standard form of the given circle is,

`(x-5)^2+(y-3)^2=(3√(2))^2`

`\implies (x-5)^2+(y-3)^2=18`