Question

What is the 15th term of the sequence 20,16,12,8,4

Answer 1

d = T2 - T1
d = 16 - 20
d = - 4

T15 = 20 + 14(-4)
= 20 - 56
= - 36

Answer 2

The nth term for the arithmetic sequence is given by:

`a_n=a_1+(n-1)d`

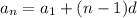
where,

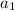`a_1` is the first term.

d is the common difference of two consecutive term.

n is the number of terms.

As per the statement:

Given the sequence:

20, 16, 12, 8, 4

This is a arithmetic sequence.

Here,
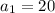`a_1=20` with common difference(d) = -4

Since,

16-20 = -4

12-16= -4

8-12 = -4

4-8 = -4

To find the 5th term of the sequence.

Substitute the given values and n = 15 we have;

`a_(15) = 20+(15-1)(-4)`

⇒
`a_(15) = 20 + (14)(-4)`

⇒
`a_(15) = 20 - 56 = -36`

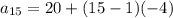
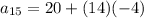
Therefore, the 5th term of the given sequence is, -36