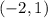Question

Given function f(x) = 2x^5+ 5x^4, use First Derivative Test to determine.a). minimum and maximum points on interval [- 2, 1]b). intervals of increase and decrease on interval (-∞, + ∞)

Answer 1

Given:

`f\mleft(x\mright)=2x^5+5x^4`

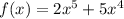
To find:

a) The minimum and maximum points on interval [- 2, 1].

b) The intervals of increase and decrease on interval

`\left(-∞,∞\right)`

Step-by-step explanation:

a) Let us find the first derivative.

`f^(\prime)(x)=10x^4+20x^3`

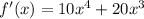
Using the first derivative test,

`\begin{gathered} f^(\prime)(x)=0 \\ 10x^4+20x^3=0 \\ 10x^3(x+2)=0 \\ x=0;x=-2 \end{gathered}`

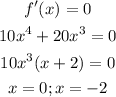
Substituting x = 0, x = -2, and x = 1 in the given equation, we get

`\begin{gathered} f(0)=0+0=0 \\ f(-2)=2(-2)^5+5(-2)^4=16 \\ f(1)=2(1)^5+5(1)^4=7 \end{gathered}`

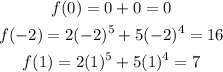
Therefore, In the interval [-2, 1],

The minimum of the function is 0 at x = 0.

The maximum of the function is 16 at x = -2.

b) Since the x values are x = -2, and x = 0

The intervals are,

`(-\infty,-2),(-2,0),(0,\infty)`

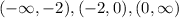
When x = -3, we get

`f^(\prime)(-3)=10(-3)^4+20(-3)^3=270>0`

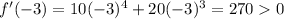
It is positive.

When x = -1, we get

`f^(\prime)(-1)=10(-1)^4+20(-1)^3=-10<0`

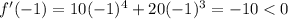
It is negative.

When x = 1, we get

`f^(\prime)(1)=10(1)^4+20(1)^3=30>0`

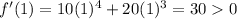
It is positive.

Therefore, the increasing intervals are

`(-\infty,-2)\cup(1,\infty)`

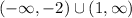
The decreasing interval is

`(-2,1)`

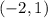
Final answer:

The minimum of the function is 0 at x = 0.

The maximum of the function is 16 at x = -2.

The increasing intervals are,

`(-\infty,-2)\cup(1,\infty)`

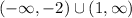
The decreasing interval is,

`(-2,1)`