Question

Two bricklayers, Sam and Joe, are working on your house. Sam can complete the work in 5 hours, while Joe can complete the work in 3 hours. How many hours does the bricklaying take if they work together?

A. 15/8
B. 15/9
C. 6/8
D. 4/3

Answer 1

3x+5x=15
8x=15
x=15/8

You need to add the two rates together, like I've shown above. Hope this helped!

Answer 2

Answer: The correct option is (A)
`(15)/(8)~\textup{hours}.`

Step-by-step explanation: Given that Sam can complete the work in 5 hours, while Joe can complete the work in 3 hours.

We are to find the number of hours they will take to complete the work if they work together.

We have

Sam can complete the work in 5 hours.

So, in 1 hour, the portion of the work Sam can complete
`(1)/(5).`

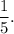
Joe can complete the work in 3 hours.

So, in 1 hour, the portion of the work Joe can complete
`(1)/(3).`

Therefore, if they work together, the portion of the work they will complete in 1 hour will be

`(1)/(5)+(1)/(3)=(3+5)/(15)=(8)/(15).`

Thus, they can complete the work in
`(15)/(8)~\textup{hours}.`

Option (A) is correct.