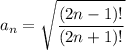
Notice that
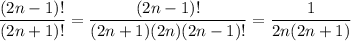
So as
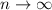
you have

. Clearly
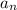
must converge.
The second sequence requires a bit more work.
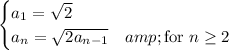
The monotone convergence theorem will help here; if we can show that the sequence is monotonic and bounded, then
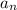
will converge.
Monotonicity is often easier to establish IMO. You can do so by induction. When
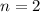
, you have
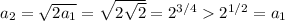
Assume

, i.e. that

. Then for
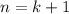
, you have
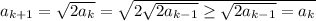
which suggests that for all

, you have
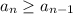
, so the sequence is increasing monotonically.
Next, based on the fact that both
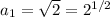
and

, a reasonable guess for an upper bound may be 2. Let's convince ourselves that this is the case first by example, then by proof.
We have
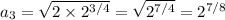
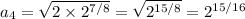
and so on. We're getting an inkling that the explicit closed form for the sequence may be

, but that's not what's asked for here. At any rate, it appears reasonable that the exponent will steadily approach 1. Let's prove this.
Clearly,

. Let's assume this is the case for
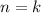
, i.e. that
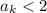
. Now for
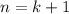
, we have

and so by induction, it follows that
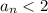
for all
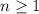
.
Therefore the second sequence must also converge (to 2).