Let the the two given supplementary angles be A & B respectively. Ratio of angle A to the ratio of angle B is 5/7. And we've been asked to find out the measure of angle A & B.
As we know that supplementary angle are the ones which have the sum of angles and tend to 180°. Thus we can write by forming equation that,
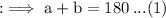
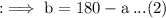
Now as per the given ratio we can write,
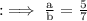
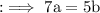
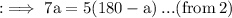

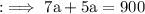
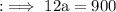
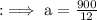
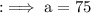
Now by equation (2) we can write,

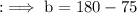
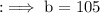
- The measure of angles are 75° and 105°.