Question

The x represents the number of items produced and sold to distributors

Answer 1

The revenue function and cost function are given as,

`\begin{gathered} R(x)=800x-x^2 \\ C(x)=2000+40x \end{gathered}`

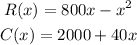
The corresponding profit function will be,

`\begin{gathered} P(x)=R(x)-C(x) \\ P(x)=(800x-x^2)-(2000+40x) \\ P(x)=800x-x^2-2000-40x \\ P(x)=-x^2+760x-2000 \end{gathered}`

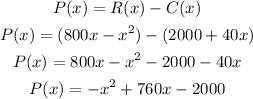
The objective is to maximize this profit function.

Differentiate the function with respect to 'x' as follows,

`\begin{gathered} P^(\prime)(x)=(d)/(dx)(-x^2+760x-2000) \\ P^(\prime)(x)=-2x+760(1)-0 \\ P^(\prime)(x)=-2x+760 \end{gathered}`

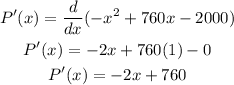
Obtain the critical points by equating the derivative to zero,

`\begin{gathered} P^(\prime)(x)=0 \\ -2x+760=0 \\ x=380 \end{gathered}`

It follows that the profit function attains an extremum when x=380.

Observe the second derivative of the function,

`\begin{gathered} P^(\prime\prime)(x)=(d)/(dx)P^(\prime)(x) \\ P^(\prime\prime)(x)=(d)/(dx)(-2x+760) \\ P^(\prime\prime)(x)=-2(1)+0 \\ P^(\prime\prime)(x)=-2 \end{gathered}`

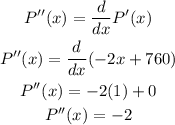
According to the Second Derivative Test, it can be concluded that the profit function attains a maximum at the obtained critical point.

(B)

Thus, the number of units that must be produced and sold to obtain maximum profit is 380.

(A)

Put this value in the profit function to obtain the value of maximum profit,

`\begin{gathered} P_(\max )=P(380) \\ P_(\max )=-(380)^2+760(380)-2000 \\ P_(\max )=142400 \end{gathered}`

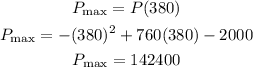
Thus, the maximum profit of the company is $142400.