Question

Find a particular solution to the nonhomogeneous differential equation y'' + 4 y = cos(2x) + sin(2x).

Answer 1

The characteristic solution follows from solving the characteristic equation,


`r^2+4=0\implies r=\pm2i`

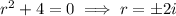
so that


`y_c=C_1\cos2x+C_2\sin2x`

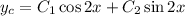
A guess for the particular solution may be
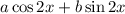
`a\cos2x+b\sin2x`, but this is already contained within the characteristic solution. We require a set of linearly independent solutions, so we can look to


`y_p=ax\cos2x+bx\sin2x`

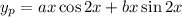
which has second derivative


`{y_p}''=(-4ax+4b)\cos2x+(-4bx-4a)\sin2x`

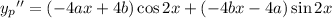
Substituting into the ODE, you have


`y''+4y=\cos2x+\sin2x`

`\implies4b\cos2x-4a\sin2x=\cos2x+\sin2x`

`\implies\begin{cases}4b=1\\-4a=1\end{cases}\implies a=-\frac14,b=\frac14`

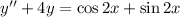
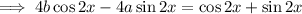
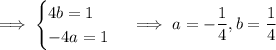
Therefore the particular solution is


`y_p=-\frac14x\cos2x+\frac14x\sin2x`

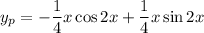
Note that you could have made a more precise guess of


`y_p=(a_1x+a_0)\cos2x+(b_1x+b_0)\sin2x`

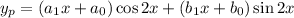
but, of course, any solution of the form
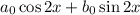
`a_0\cos2x+b_0\sin2x` is already accounted for within
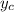
`y_c`.