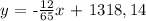Question:
Solution:
The slope-intercept form of the line is given by the following equation:
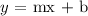
where m is the slope of the line and b is the y-coordinate of the y-intercept of the line. Now, to find the slope of a line we use the following equation:
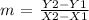
where (X1,Y1) and (X2,Y2) are points on the line. In this case, we can take the points:
(X1,Y1) = (797, 1171)
(X2,Y2) = (1122, 1111)
now, replace this data into slope equation:

then, temporarily we have that the equation of the given line is

to find b, replace any point (x,y) on the line, in the above equation, and solve for b. For example, take (x,y) = (797, 1171), then we get:
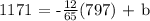
this is equivalent to say:
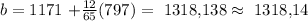
then, we can conclude that the slope-intercept form for the given line is: