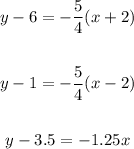Question

Which equations represent the days in the table? check all that apple

Answer 1

`\begin{gathered} y-6=-(5)/(4)(x+2) \\ \\ y-1=-(5)/(4)(x-2) \\ \\ y-3.5=-1.25x \end{gathered}`

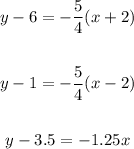
Step-by-step explanation

We want to find the equation that represents the data in the given table.

The table represents a linear relationship between x and y. This implies that the equation representing the table (in point-slope) form can be written generally as:

`y-y_1=m(x-x_1)`

where m = slope

(x1, y1) = a pair of points from the table

First, we have to find the slope, m, by using two pairs of points from the table and applying the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Let us use the points (-2, 6) and (2, 1):

`\begin{gathered} m=(1-6)/(2-(-2))=(1-6)/(2+2) \\ \\ m=(-5)/(4) \\ \\ m=-(5)/(4) \end{gathered}`

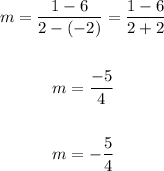
Now, substitute the values for m and (x1, y1) into the point-slope formula:

`\begin{gathered} y-6=-(5)/(4)(x-(-2)) \\ \\ y-6=-(5)/(4)(x+2) \end{gathered}`

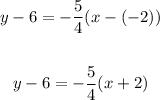
We can also use another pair of points on the table for (x1, y1). Let us use (2, 1):

`y-1=-(5)/(4)(x-2)`

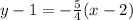
Also, we can simplify either equation as follows:

`\begin{gathered} y-6=-(5)/(4)x-(5)/(2) \\ \\ y-6=-1.25x-2.5 \\ \\ y-6+2.5=-1.25x \\ \\ y-3.5=-1.25x \end{gathered}`

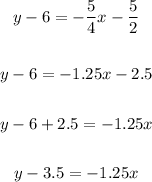
Therefore, the correct options are:

`\begin{gathered} y-6=-(5)/(4)(x+2) \\ \\ y-1=-(5)/(4)(x-2) \\ \\ y-3.5=-1.25x \end{gathered}`