Question

Finding the direction of the sum of the 2 vectors

Answer 1

To find the direction of the sum let's first find the sum, to do this we need to perform the vector decomposition:

`\vec{A}=85\hat{i}`

and

`\vec{B}=101\cos 60\hat{i}+101\sin 60\hat{j}`

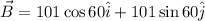
Adding the vectors we have:

`\begin{gathered} \vec{A}+\vec{B}=85\hat{i}+(101\cos 60\hat{i}+101\sin 60\hat{j}) \\ \vec{A}+\vec{B}=(85+101\cos 60)\hat{i}+101\sin 60\hat{j} \\ \vec{A}+\vec{B}=135.5\hat{i}+87.47\hat{j} \end{gathered}`

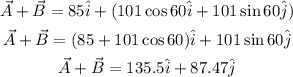
Now we need to remember that the angle of the vector is given by:

`\theta=\tan ^(-1)((v_y)/(v_x))`

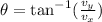
where vx and vy are the x-component and y-component, respectively. Plugging the values we found we have that:

`\begin{gathered} \theta=\tan ^(-1)((87.47)/(135.5)) \\ \theta=32.84 \end{gathered}`

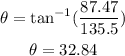
Therefore, the direction of the sum is 32.84°