Question

(Extra Credit) Eighty percent of the light aircraft that disappear while in flight in a certain country are subsequently discovered. Of the aircraft that are discovered, 75% have an emergency locator, whereas 90% of the aircraft not discovered do not have such a locator. Suppose a light aircraft has disappeared. If it has an emergency locator, what is the probability that it will not be discovered?

Answer 1

0.0323 = 3.23% probability that it will not be discovered

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

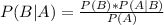
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Has emergency locator

Event B: Probability it will not be discovered.

Eighty percent of the light aircraft that disappear while in flight in a certain country are subsequently discovered.

So 20% are not discovered, which means that
`P(B) = 0.2`.

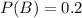90% of the aircraft not discovered do not have such a locator.

So 10% of the aircraft discovered have the location, which means that
`P(A|B) = 0.1`

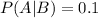
Probability of having the locator:

75% of 80%(Discovered).

10% of 20%(Not discovered). So

`P(A) = 0.75*0.8 + 0.1*0.2 = 0.62`

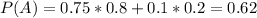
If it has an emergency locator, what is the probability that it will not be discovered?

`P(B|A) = (P(B)*P(A|B))/(P(A)) = (0.2*0.1)/(0.62) = 0.0323`

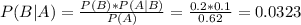
0.0323 = 3.23% probability that it will not be discovered