Question

Ap calculus ab. I'm completely lost

Answer 1

`\displaystyle f'(0) = (4)/(3)`

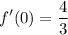
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Terms/Coefficients
• Factoring
• Functions
• Function Notation
• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

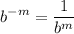
Calculus

Derivatives

Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Step-by-step explanation:

Step 1: Define

Identify

`\displaystyle f(x) = (x^2 - 2x - 1)^\bigg{(2)/(3)}`

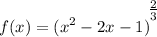
Step 2: Differentiate

1. Chain Rule:
   `\displaystyle f'(x) = (d)/(dx)[(x^2 - 2x - 1)^\bigg{(2)/(3)}] \cdot (d)/(dx)[(x^2 - 2x - 1)]`
2. Basic Power Rule {Derivative Property - Subtraction]:
   `\displaystyle f'(x) = (2)/(3)(x^2 - 2x - 1)^\bigg{(2)/(3) - 1} \cdot (2x^(2 - 1) - 2x^(1 - 1) - 0)`
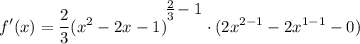
3. Simplify:
   `\displaystyle f'(x) = (2)/(3)(x^2 - 2x - 1)^\bigg{(-1)/(3)} \cdot (2x - 2)`
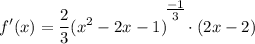
4. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle f'(x) = \frac{2(2x - 2)}{3(x^2 - 2x - 1)^\bigg{(1)/(3)}}`
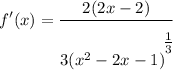
5. Factor:
   `\displaystyle f'(x) = \frac{4(x - 1)}{3(x^2 - 2x - 1)^\bigg{(1)/(3)}}`

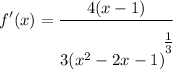
Step 3: Evaluate

1. Substitute in x [Derivative]:
   `\displaystyle f'(0) = \frac{4(0 - 1)}{3[0^2 - 2(0) - 1]^\bigg{(1)/(3)}}`
2. [Order of Operations] Simplify:
   `\displaystyle f'(0) = (4)/(3)`

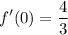
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e