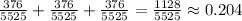Answer: 1128/5525 = 0.204
There are 52 cards in one deck. First, we list down all the probabilities of picking exactly one ace for each deal:
Getting an ace as the first card:
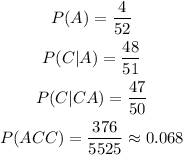
Then, we will find the probability of getting an ace as the second card:
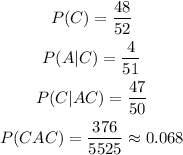
Then, the probability of getting an ace on the third card:
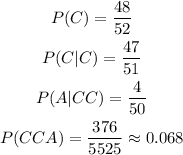
We will then add all of these probabilities: