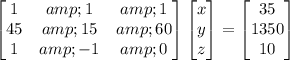Question

To help passengers stranded by bad weather one winter, an airport bought cots, chairs, and tables totaling 35. They bought cots at $45 each, chairs for $15 each, and tables for $60 each. They spent a total of $1350 on the furniture. The number of chairs they purchased was 10 less than the number of cots. Set up a system and an augmented matrix to solve for the number of each type of furniture pieces the airport purchased.

Answer 1

The system of matrix needed to solve the problem will be;

`\begin{bmatrix}{1} & {1} & {1} \\ {45} & {15} & {60} \\ {1} & {-1} & {0}\end{bmatrix}\begin{bmatrix}{x} \\ {y} \\ {z}\end{bmatrix}=\begin{bmatrix}{35} \\ {1350} \\ {10}\end{bmatrix}`

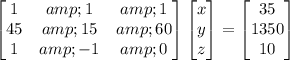
Step-by-step explanation:

Let x, y and z represent the number of cots, chairs, and tables the airport bought.

Given;

The airport bought cots, chairs, and tables totaling 35. the total number of cots, chairs and tables bought is 35. So, we have;

`x+y+z=35\text{ ---------1}`

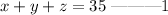
If they bought cots at $45 each, chairs for $15 each, and tables for $60 each. And they spent a total of $1350 on the furniture.

Then the total cost is the sum of the cost of each type of furniture;

`45x+15y+60z=1350\text{ ----------2}`

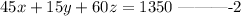
And also, The number of chairs they purchased was 10 less than the number of cots. So, we have;

`\begin{gathered} y=x-10 \\ x-y=10\text{ --------3} \end{gathered}`

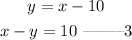
So we have the three equations needed.

We can combine the 3 equations to form a matrix.

Therefore, the system of matrix needed to solve the problem will be;

`\begin{bmatrix}{1} & {1} & {1} \\ {45} & {15} & {60} \\ {1} & {-1} & {0}\end{bmatrix}\begin{bmatrix}{x} \\ {y} \\ {z}\end{bmatrix}=\begin{bmatrix}{35} \\ {1350} \\ {10}\end{bmatrix}`