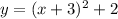Question

Complete the square to find the equation of the parabola in the problem y = x^2 + 6x + 11 in standard form.

Answer 1

When we are given a quadratic expression in the standard form:

`y=ax^2+bx+c`

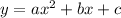
We can complete the squares to rewrite it as:

`y=a(x+d)^2+e`

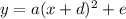
Where:

`\begin{gathered} d=(b)/(2a) \\ . \\ e=e-(b^2)/(4a) \end{gathered}`

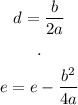
The poroblem gives us the quadratic equation:

`y=x^2+6x+11`

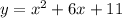
Here, we have:

a = 1

b = 6

c = 11

Let's calculate d and e:

`\begin{gathered} d=(6)/(2\cdot1)=3 \\ \end{gathered}`
`e=11-(6^2)/(4\cdot1)=11-(36)/(4)=2`

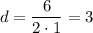
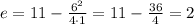
Then, we can rewrite:

`y=1(x+3)^2+2`

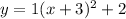
Thus, the answer is:

`y=(x+3)^2+2`