Question

The length of a social media interaction is normally distributed with a mean of 3 minutes and a standard deviation of 0.4 minutes. What is the probability that an interaction lasts longer than 4 minutes?

Answer 1

z = (4 - 3)/.4
z = 1/.4
z = 2.5
.0062

Answer 2

Answer would be 0.00621

Explanation:

It given that the length of a social media interaction is normally distributed with a mean of 3 minutes and standard deviation of 0.4 minutes.

The probability that a randomly selected data, X, is greater than a given value, x, is given by

`P(X \ \textgreater \ x)=P \left(z\ \textgreater \ (x-\mu)/(\sigma) \right)=1-P \left(z\ \textless \ (x-\mu)/(\sigma) \right)`

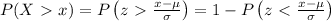
The probability that an interaction lasts longer than 4 minutes is given by

`P(X\ \textgreater \ 4)=P\left(X\ \textgreater \  (4-3)/(0.4) \right) </p><p> =P(X\ \textgreater \ 2.5)=1-P(X\ \textless \ 2.5)`

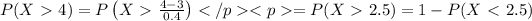
Now using normal distribution table (z table) or calculator to evaluate that

P(X< 2.5) = 0.99379

Therefore the probability that an interaction lasts longer than 4 minutes

= 1 - 0.99379 = 0.00621