Question

" 5 Explain if the triangles are similar using SAS-. If they are similar, which angles are congruent and how do you know? 1: (Explain your reasoning using evidence like a paragraph proof NOT a rigid motion proof!)

Answer 1

The two triangles are similar according to the SAS requirement for similar triangles.

The two angles that are congruent are JFS and PFT

Angle JFS = Angle PFT (Vertically opposite angles are equal)

Check Explanation

Step-by-step explanation

SAS indicates that the two triangles are similar according the the Side-Angle-Side theorem which explains that the two triangles will each have two sides that are similar (ratio of corresponding sides would be the same) and then, the two triangles will each have an included angle (an angle in between those similar sides) being equal in measure.

So, to check for these two triangles, we check for the angle and the sides that are supposed to be similar.

For the angle, we can tell that

Angle JFS = Angle PFT (Vertically opposite angles are equal)

Then, for the sides, we can tell that

PT is corresponding to JS

FT is corresponding to JF

So, if the sides are similar, the ratios of these corresponding sides should be equal.

`(PT)/(JS)=(25)/(40)=0.625`
`(FT)/(JF)=(27.5)/(44)=0.625`

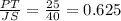
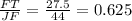
Since 0.625 = 0.625

We can see that the two triangles satisfy the SAS requirement for the two triangles to be similar.

Hope this Helps!!!