Answer:
0.15 g of CuSO4.
Step-by-step explanation:
What is given?
Concentration of CuSO4 = 0.00095 mol/L.
Liters of solution = 1 L.
RAM (Cu) = 63.
RAM (S) = 32.
RAM (O) = 16.
Step-by-step solution:
Let's see the formula of molarity (concentration of solution):
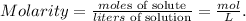
And we want to find the moles of solute to calculate the weight of copper sulfate. The statement is telling us that we're going to use 1 liter of solution, so let's solve for 'moles of solute' and replace the given data (molarity of CuSO4 solution = concentration of CuSO4 = 0.00095 mol/L and liters of solution = 1L):
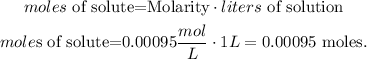
Now, we have to convert 0.00095 moles of CuSO4 to mass and here we're going to use the RAM (relative atomic mass)
First, let's calculate the RAM of CuSO4 by doing an algebraic sum with the given RAMs. You can see that we have 1 Cu, 1 S, and 4 O, so the calculation will look like this:
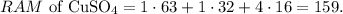
The RAM of CuSO4 is 159. The value of RAM is equivalent to molar mass, but the difference is that the molar mass has the units of g/mol, so, in this case, the molar mass of CuSO4 is 159 g/mol. So now, the conversion from moles to grams will be:
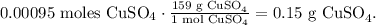
The answer is that they have to weigh out 0.15 g of CuSO4.