Question

The population of a type of local bass can be found using an infinite geometric series where a1 = 94 and the common ratio is one third. Find the sum of this infinite series that will be the upper limit of this population.

Answer 1

a/(1-r)

a = 94

r = 1/3

94/(1-1/3)

= 141

Answer 2

The sum of this infinite series that will be the upper limit of this population is, 141

Explanation:

Formula for infinite geometric series is given by:

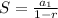`S = (a_1)/(1-r)` ....[1]

where,

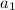`a_1` is the first term,

r is the common ratio term.

As per the statement:

The population of a type of local bass can be found using an infinite geometric series where:

`a_1 = 94`

`r = (1)/(3)`

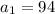
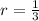
To find the sum of this infinite series that will be the upper limit of this population.

Substitute the given values in [1] we have;

`S = (94)/(1-(1)/(3)) = (94)/((2)/(3)) = 94 \cdot (3)/(2) = 47 \cdot 3 = 141`

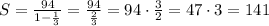
Therefore, 141 is the sum of this infinite series that will be the upper limit of this population.