Question

The segments in each figure are tangent to the circle. Solve for y and then find thelength of the indicated segment.S5yРR3y + 4T

Answer 1

`\begin{gathered} y=2 \\ RS=RT=10 \end{gathered}`

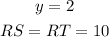
Explanation:

The two tangent theorem states that if there are two lines from the same point which lies outside a circle, such that both lines are tangent to the circle, then their lengths are the same. This can be represented by the following:

Therefore, we can equalize the expressions of the lengths to find y:

`5y=3y+4`

Solve for y.

`\begin{gathered} 5y-3y=4 \\ 2y=4 \\ y=(4)/(2) \\ y=2 \end{gathered}`

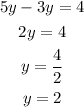
Hence, to calculate the length of the indicated segments, we need to substitute y=2 into the expressions:

`\begin{gathered} RS=5y \\ RS=10 \\ \\ RT=3y+4 \\ RT=3(2)+4 \\ RT=10 \end{gathered}`