Question

Part a is already complete, answer is (2p+12)/13 + (3p-8)i/13. need help with part b

Answer 1

We are given a complex number of the form:

`w=(2p+12)/(13)+(3p-8)/(13)i`

We are also given that arg(w) = π/4. With this information, we can calculate the value of p.

The argument of a complex number is defined as:

`\tan w=(y)/(x)`

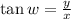
Where y and x are the imaginary and real parts (respectively) of the complex number. Applying the formula:

`\tan (\pi)/(4)=((3p-8)/(13))/((2p+12)/(13))`

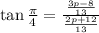
Since the tangent of π/4 is 1, the real and the imaginary parts happen to be equal, that is:

`\begin{gathered} ((3p-8)/(13))/((2p+12)/(13))=1 \\ (3p-8)/(13)=(2p+12)/(13) \end{gathered}`

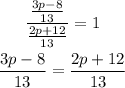
Simplifying by 13:

`\begin{gathered} 3p-8=2p+12 \\ \text{Simplifying:} \\ 3p-2p=12+8 \\ \text{Solving:} \\ p=20 \end{gathered}`

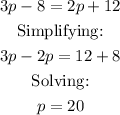
Substituting into the complex number:

w = 3 + 3i